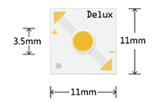
【技术专区】LED 封装器件芯片结温测试浅述(下)
摘要: 假设热源到环境的导热只有一个路径,而且是一种材料,这种材料是各向同性而且形状规则,有一定的热阻与热容,习惯上我们也同样用电阻电容的符号来代表热阻和热容,热源从材料的左表面流到右表面(环境),可以看到这样的一个RC(阻容)网络。
大家应该还记得在《LED 封装器件芯片结温测试浅述(上)》里面我们有提及到
“电流跳变”的瞬态测试方法,如果我们在跳变之后不断地采集电压信号,直到器件冷却到环境温度,我们就可以得到LED在降温过程中它的电压随时间的变化曲线,又因为这些电压变化都是在测试电流下得到的,我们只需要把电压信号除以K系数就可以得到温度变化随时间的曲线(因为k=Δv/Δt),温度变化曲线如图1所示:

图1 温度变化-时间曲线
时间对数化
事实上,图1中的时间轴是经过对数化处理的,因为实际进行采样时我们是得益于设备的高速采样可以在1μs(即10-6s)后采集到第一个电压的变化值,但采样总时间的数量级一般都在1s~103s范围内,时间的数量级跨度大而且时间越往后温度变化就越慢,数据的重要度也随之降低,因此在数据处理时我们把时间进行对数化处理。时间对数化后的曲线如图2b所示。
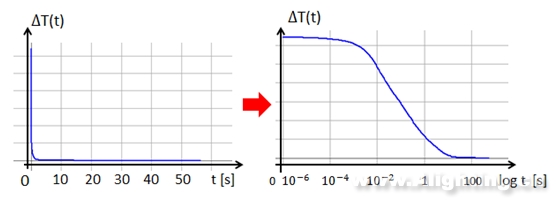
图2a温度变化响应曲线 图2b温度变化响应曲线(时间对数化后)
对比图2a和图2b可以发现,对数前处理前的数据变化不直观,对数化处理后却能把瞬态切换后几微秒内的温度变化充分表示出来。后文在计算中也要用到时间对数化的推导。
这次我们就用这个曲线来获得我们神奇的结构函数。首先要介绍一下:
阻容网络的物理模型
首先,我们需要构造一个导热的模型。不如先从简单开始,假设热源到环境的导热只有一个路径,而且是一种材料,这种材料是各向同性而且形状规则,有一定的热阻与热容,习惯上我们也同样用电阻电容的符号来代表热阻和热容,热源从材料的左表面流到右表面(环境),如图3所示。
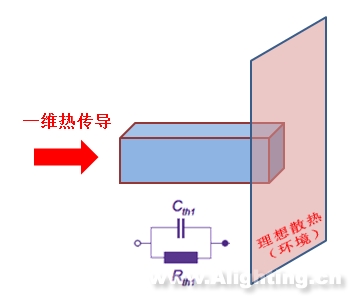
图3热传导模型图示及RC网络
在这个简单的模型里,我们看到这样的一个RC(阻容)网络,如图4,在这个网络里,热源当作一个恒流源,而热阻与热容并联到环境,我们称之为一阶RC网络。
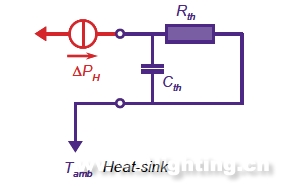
图4 一阶RC网络
在数字信号处理领域,通常都是利用一个系统的响应再把系统的结构分析出来。所谓响应就是系统在某一特定信号源的激励下产生的反应(输出特性),比如有人在你身后喊了一声你的名字,有的人会回头望而有的人不回头只是应了一声。不同的系统会有不同的响应,同一个系统在不同信号的激励下也会有不同的响应。
现在我们把这个一阶RC网络看成一个系统,那要用什么信号做激励呢?其实文初我们提到的“电流跳变”就可以做为一个信号源,一般我们把这种电流跳变信号称为单位阶跃信号,因为它的信号就像台阶一样突然从低跳到高(或从高到低),那这个系统在单位阶跃信号激励下的响应是怎样的呢?
如果输入信号是单位阶跃信号,则这个系统的响应我们简称为该系统的单位阶跃响应。
那么一阶RC网络的单位阶跃响应为


图5 一阶RC网络及对应的时间常数图
式1中的 τ我们称为时间常数,它是信号处理领域里的常用的表征时间的物理量,其量纲单位和时间一样,也是秒[s]。时间常数的含义是指某物理量从最大值衰减到最大值的1/e(或从最小值增加到最大值的1-1/e倍)所需要的时间,比如一个满电荷的电容两端并联一个电阻,那么电容两端的电压从最大值放电到最大值的1/e倍所花的时间就是 。
这里我们称τ为“热时间常数”以示区分,因为它代表的是热阻与热容的乘积。
现在我们把结构的数量从1个升级到n个,那么就会变成n阶RC网络,如图6所示。
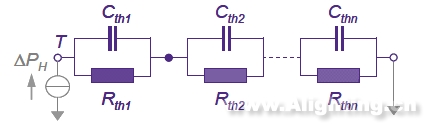
图6 n阶RC网络
其对应的单位阶跃响应为
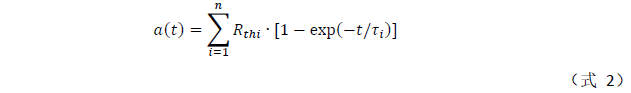
一般我们把这种结构的RC网络称为n阶福斯特(Foster)结构,其对应的热时间常数谱如图7所示。
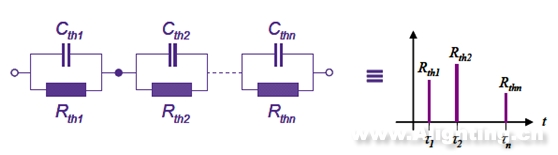
图7 n阶福斯特结构的热时间常数图
实际上,材料与材料之间的交接界面是同样存在热阻与热容的,器件各材料之间也不可能完全看成独立成单一的热阻热容,我们应该认为热阻与热容的变化是连续的,于是我们需要把这个离散的多项式进行连续化处理,也就是当n趋向于正无穷的时候,可把(式2)改为
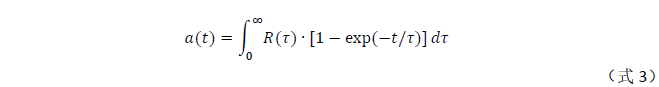
(式3)中的R(τ)称为时间常数谱函数,我们用连续的R(τ)来取代离散的Rthi 。它的时间常数图为连续谱图,如图8所示。

图8 连续谱图
(式3)这个公式代表的就是一个连续RC网络的单位阶跃响应。
看回文初的图1b温度变化曲线,事实上这个曲线在对数化处理前对应的表达式就是

凡注明为其它来源的信息,均转载自其它媒体,转载目的在于传递更多信息,并不代表本网赞同其观点及对其真实性负责。
用户名: 密码: